Table of Contents
What is Kalman Filter(KF)?
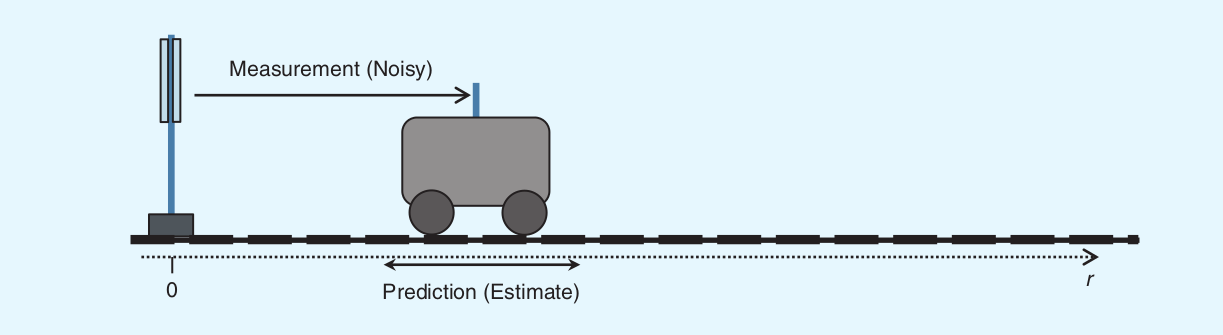
对于某一个系统,假定知道当前状态\(X_{t-1}\),存在以下两个问题:
- 经过时间\(\Delta t\)后,下一个状态\(X_{t}\)如何求出?
- 假定已求出\(X_{t}\),同时在\(t\)时刻接收到传感器的非直接信息\(Z_{t}\),如何利用\(Z_{t}\)来对状态\(X_{t}\)进行修正呢?
以上两个问题就是卡尔曼滤波要解决的,可以简要概括如下:
As an example
以一维运动为例,假定有一个小车,开始位于\(x=\mu_1\)的位置,但是由于误差的存在,其真实分布是高斯分布,其方差是\(\sigma_{1}^{2}\),即其原始位置分布是\(N(\mu_1,\sigma_{1}^{2})\),当该小车经过运动,到达终点位置,但是由于运动也是不准确的(受轮胎打滑等因素影响),其移动过程的分布也是高斯分布,移动分布为\(N(\mu_2,\sigma_{2}^{2})\),那么其最终的位置分布是怎样的呢?
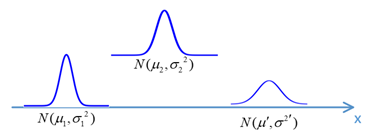
这是一个预测过程,求预测位置符合全概率法则,即:
$ N(\mu',{\sigma'}^2)=N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2) \tag{1} \label{eq1}$
考虑另外一种情况,同样是一维运动,有一个小车开始时位于\(x=\mu_1\)的位置,但由于误差的存在,其真实分布是方差为\(\sigma_1^2\)的高斯分布,即其开始位置的分布为\(N(\mu_1,\sigma_{1}^{2})\),此时有一个传感器检测到该小车位于\(x=\mu_2\),分布的方差为\(\sigma_2^2\),那么小车的真实分布是多少呢?
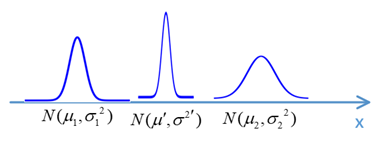
这是一个感知过程,其符合贝叶斯法则,最终分布是两个分布相乘,即:
$ N(\mu',{\sigma'}^2)=N(\mu_1,\sigma_1^2) \times N(\mu_2,\sigma_2^2)=N(\frac{\mu_1\sigma_2^2+\mu_2\sigma_1^2}{\sigma_1^2+\sigma_2^2},\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}) \tag{2} \label{eq2}$
One step further
下面将感知过程中的利用到的贝叶斯法则扩展到多维,这也是卡尔曼滤波的核心。
已知在一维模式下,两个分布融合得到的均值和方差分别为:
$
\mu'=\frac{\mu_1\sigma_2^2+\mu_2\sigma_1^2}{\sigma_1^2+\sigma_2^2}=\mu_1+\frac{\sigma_1^2(\mu_2-\mu_1)}{\sigma_1^2+\sigma_2^2}
$
$
{\sigma'}^2=\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}=\sigma_1^2-\frac{\sigma_1^4}{\sigma_1^2+\sigma_2^2}
$
我们令
$
K=\frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2}
$
则有:
$
\mu'=\mu_1+K(\mu_2-\mu_1)
$
$
{\sigma'}^2=\sigma_1^2-K\sigma_1^2
$
将该结果扩展到多维情况下,得到:
$
\pmb{K}=\Sigma_1(\Sigma_1+\Sigma_2)^{-1}
$
$
\pmb{\mu'}=\mu_1+\pmb{K}(\mu_2-\mu_1) \tag{3} \label{eq3}
$
$
\Sigma'=\Sigma_1-\pmb{K}\Sigma_1
$
该公式会在卡尔曼滤波的修正更新过程中用到。
Multi-dimention
考虑一个二维状态的例子:
已知小车在\(t\)时刻的状态\(\pmb{X_{t}}\),其表示为一个拥有2个分量的向量,分量分别表示位置信息\(p\)和速度信息\(v\),即:
$
\pmb{X_{t}}=\begin{bmatrix}p\\
v \end{bmatrix}
=\begin{bmatrix}x_{t}\\
\dot{x_{t}} \end{bmatrix}
$
但这个状态不一定准确,其不确定性用协方差矩阵表示(为什么?):
$
\pmb{P_{t}}=\begin{bmatrix}\Sigma_{pp}&\Sigma_{pv}\\
\Sigma_{vp}&\Sigma_{vv} \end{bmatrix}
$
Prediction
将加速度等视作外部因素,只考虑小车本身的运动,有:
$
x_{t}=x_{t-1}+ \dot{x}_{t-1}\Delta t
$
$
\dot{x}_{t}=\qquad \quad \dot{x}_{t-1} \quad
$
用矩阵表示:
$
\pmb{\hat{X}_{t}}=\begin{bmatrix} 1 &\Delta t\\
0 & 1 \end{bmatrix} \pmb{\hat{X}_{t-1}}
=\pmb{F} \pmb{\hat{X}_{t-1}}
$
注:考虑\(\Delta t\)为常量,此时状态转换矩阵\(F_t\)不变,故简写为\(F\),下同。
在状态变化的过程中引入了新的不确定性,根据协方差的乘积公式:
$
Cov(x)=\Sigma
$
$
Cov(\pmb{A}x)=\pmb{A}\Sigma\pmb{A}^T \tag{4} \label{eq4}
$
可得:
$
\pmb{\hat{X}_{t}} = \pmb{F} \pmb{\hat{X}_{t-1}}
$
$
\pmb{P_{t}} = \pmb{F} \pmb{P_{t-1}}\pmb{F}^T
$
考虑外部因素\(\pmb{u_{t-1}}\),如引入加速度 \(a_{t-1} = \ddot{x}_{t-1}\):
$
x_{t}=x_{t-1}+ \dot{x}_{t-1}\Delta t + \frac{1}{2} \ddot{x}_{t-1} \Delta t^2
$
$
\dot{x}_{t}=\qquad \quad \dot{x}_{t-1} \quad+\quad \ddot{x}_{t-1} \Delta t
$
写成矩阵形式:
$
\pmb{\hat{X}_{t}} = \pmb{F} \pmb{\hat{X}_{t-1}} + \begin{bmatrix} \frac{1}{2} \Delta t^2\\
\Delta t \end{bmatrix} \ddot{x}_{t-1}
$
$
= \pmb{F} \pmb{\hat{X}_{t-1}} + \pmb{B}\pmb{u_{t-1}} \quad
$
同时,还存在环境误差,以\(\pmb{Q_{t-1}}\)表示。最终预测的形式呈现为:
$
\pmb{\hat{X}_{t}} = \pmb{F} \pmb{\hat{X}_{t-1}} + \pmb{B} \pmb{u_{t-1}}
$
$
\pmb{P_{t}} = \pmb{F} \pmb{P_{t-1}}\pmb{F}^T + \pmb{Q_{t-1}}
$
小结:
- 新的最优估计是之前最优估计的预测加上已知的外界影响的修正。
- 新的不确定度是预测的不确定度加上环境的不确定度。
Correction
通过预测过程我们已经得到了\(\pmb{X_{t}}\)和\(\pmb{P_{t}}\)。下一步我们要通过观测到的测量值\(\pmb{Z_{t}}\)对\(\pmb{X_{t}}\)和\(\pmb{P_{t}}\)进行修正更新。由于这个过程不再涉及\(t-1\)时刻的状态和误差,因此将\(\pmb{X_{t}}\)、\(\pmb{P_{t}}\)和\(\pmb{Z_{t}}\)省略为\(\pmb{X}\)、\(\pmb{P}\)和\(\pmb{Z}\),以方便阅读。
由于传感器观测得到的数据信息\(\pmb{Z}\)与\(\pmb{X}\)的尺度不尽相同,因此我们需要一个转换矩阵\(\pmb{H}\)将\(\pmb{X}\)转换为\(\pmb{Z}\)的尺度,即:
$
\pmb{\hat{Z}} = \pmb{H} \pmb{\hat{X}}
$
借助公式$\eqref{eq4}$,有:
$
\pmb{\Sigma} = \pmb{H} \pmb{P} \pmb{H}^T
$
目前,我们得到了\(\vec{x}\)方向(1-D)上的两个分布:
- 预测(Prediction)值\(\pmb{X}\)的分布\(N(\vec{x};\mu_1,\sigma_1^2)\)
- 测量(Measurement)值\(\pmb{Z}\)的分布\(N(\vec{x};\mu_2,\sigma_2^2)\)

在修正过程中,这两个分布融合得到\(\pmb{X'}\),记其分布为\(N_{fused}\),由公式$\eqref{eq2}$得到:
$
N_{fused}(\vec{x};\mu_{fused},\sigma_{fused}^2) = N(\vec{x};\mu_1,\sigma_1^2) \times N(\vec{x};\mu_2,\sigma_2^2)
$
扩展到二维情况,由公式$\eqref{eq4}$,我们得到:
- 预测(Prediction)值\(\pmb{X}\)对应的均值和协方差为\((\pmb{\mu_1},\Sigma_1)=(\pmb{H \hat{X}},\pmb{HPH^T})\)
- 测量(Measurement)值\(\pmb{Z}\)对应的均值和协方差为\((\pmb{\mu_2},\Sigma_2)=(\pmb{Z},\pmb{R})\)
借助公式$\eqref{eq3}$,有:
$
\pmb{HX'} = \pmb{HX} + \pmb{K} (\pmb{Z}-\pmb{HX})
$
$
\pmb{HP'H^T} = \pmb{HPH^T} - \pmb{K}\pmb{HPH^T}
$
其中,
$
\pmb{K} = \pmb{HPH^T(HPT^T+R)^{-1}}
$
将第二个式子左乘\(\pmb{H^{-1}}\);第三个式子左乘\(\pmb{H^{-1}}\),右乘\(\pmb{(H^T)^{-1}}\),得到:
$
\pmb{X'} = \pmb{X} + \pmb{K'} (\pmb{Z}-\pmb{HX})
$
$
\pmb{P'} = \pmb{P} - \pmb{K'}\pmb{HP}
$
其中,
$
\pmb{K'} = \pmb{PH^T(HPT^T+R)^{-1}}
$
\(\pmb{X'}\)和\(\pmb{P'}\)就是经过测量、更新之后的状态和不确定性,至此,卡尔曼滤波的一步就完成了。以此为基础进行不断迭代,就可以用卡尔曼滤波实现系统的定位。
To sum up
整个过程中,卡尔曼滤波共有5个公式,分别为预测过程的2个公式和测量修正过程的3个公式:
$
\pmb{\hat{X}_{t}} = \pmb{F} \pmb{\hat{X}_{t-1}} + \pmb{B} \pmb{u_{t-1}}
$
$
\pmb{P_{t}} = \pmb{F} \pmb{P_{t-1}}\pmb{F}^T + \pmb{Q_{t-1}}
$
$
\pmb{K'} = \pmb{PH^T(HPT^T+R)^{-1}}
$
$
\pmb{X'} = \pmb{X} + \pmb{K'} (\pmb{Z}-\pmb{HX})
$
$
\pmb{P'} = (1 - \pmb{K'}\pmb{H})\pmb{P}
$
What’s more?
如果考虑系统的运动是非线性的情况呢?这时我们不能再简单地用\(x=vt\)来描述系统的运动。自然地,引出非线性系统下的卡尔曼滤波——扩展卡尔曼滤波(EKF)。
此外,还有卡尔曼滤波的诸多变体,如UKF、CKF、QKF、MSCKF等等,基于扩展卡尔曼滤波的SLAM模型EKFSLAM……




